MEDIDAS DE TENDENCIA CENTRAL PARA DATOS SIMPLES Y AGRUPADOS

Se utilizan en estadística para describir ciertos comportamientos de un grupo de datos suministrados, como por ejemplo a qué valor están cercanos, cuál es el promedio de los datos recogidos, entre otros.Cuando se toma una cantidad grande de datos, es útil agruparlos para tener un mejor orden de los mismos y así poder calcular ciertas medidas de tendencia central.Entre las medidas de tendencia central más utilizadas están la media aritmética, la mediana y la moda. 

1- Media aritmética

La media aritmética consiste en multiplicar cada frecuencia por el promedio del intervalo. Luego se suman todos estos resultados, y por último se divide entre el total de datos.

Utilizando el ejemplo anterior se obtendría que la media aritmética es igual a:

(4*2 + 4*4 + 6*6 + 4*8) / 18 = (8+16+36+32)/18 = 5,11111

Esto indica que el valor medio de los datos de la tabla es 5,11111.

EJEMPLO:

✓ Ejemplo 1: En el primer examen saqué una nota de 8 y en el segundo un 10. ¿Cuál es la media aritmética de mis notas?

• Nota 1 = 8
• Nota 2 = 10
• Número de notas = 2
• Media Aritmética = (8 + 10) / 2 = 18 / 2 = 9 → He sacado una media aritmética de 9 en mis dos notas

✓ Ejemplo 2: En un experimento hemos obtenido los siguientes valores: 10, 11, 10, 9, 10, 10. Calcuar la media aritmética de los valores del experimento:

• Número de valores del experimento: 6 valores de muestra
• Media Aritmética = (10 + 11 + 10 + 9 + 10 + 10) / 6 = 60 / 6 = 10

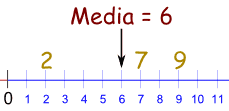
2- Mediana

Para calcular la mediana de un conjunto de datos primero se ordenan todos los datos de menor a mayor. Se pueden presentar dos casos:

– Si el número de datos es impar, entonces la mediana es el dato que está justo en el centro.

– Si el número de datos es par, entonces la mediana es el promedio de los dos datos que quedan en el centro.

EJEMPLO:

Encuentre la mediana del conjunto {3, 10, 36, 255, 79, 24, 5, 8}.

Primero, arregle los números en orden ascendente.

{3, 5, 8, 10, 24, 36, 79, 255}

Hay 8 números en el conjunto - un número par. Así, se encuentra el promedio de los dos números medios, 10 y 24.

(10 + 24) / 2 = 34/2 = 17

Así, la mediana es 17.

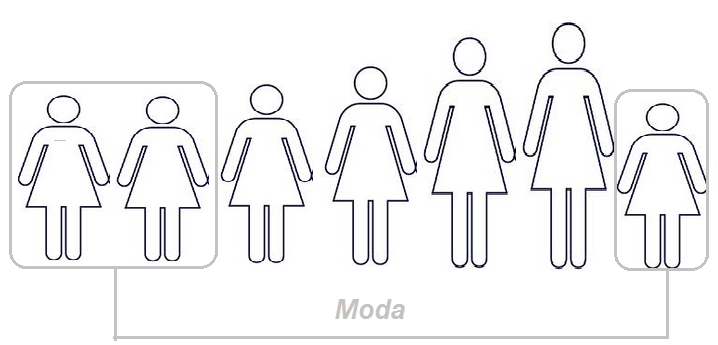
3- Moda

La moda es el valor que tiene mayor frecuencia entre todos los datos agrupados; es decir, es el valor que se repite más veces en el conjunto de datos inicial.Se hablará de una distribución bimodal de los datos adquiridos en una columna cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Una distribución trimodal de los datos es en la que encontramos tres modas. En el caso de la distribución uniforme discreta, cuando todos los datos tienen la misma frecuencia, se puede definir las modas como indicado, pero estos valores no tienen utilidad.

EJEMPLO 1:

Encuentra la moda del conjunto {2, 3, 5, 5, 7, 9, 9, 9, 10, 12}.

El 2, 3, 7, 10 y 12 aparecen una vez cada uno.

El 5 aparece dos veces y el 9 aparece tres veces.


Así, el 9 es la moda.
4.- SESGO

En estadística se llama sesgo de un estimador a la diferencia entre su esperanza matemática y el valor numérico del parámetro que estima. Un estimador cuyo sesgo es nulo se llama insesgado o centrado.

En notación matemática, dada una muestra ${\displaystyle x_{1},\dots ,x_{n}}$ y un estimador ${\displaystyle T(x_{1},\dots ,x_{n})\,}$ del parámetro poblacional ${\displaystyle \theta \,}$, el sesgo es:

BIBIOGRAFÍA 

https://www.vitutor.net/2/11/moda_media.html

https://es.plusmaths.com/la-mediana-en-estadistica.html

https://es.m.wikipedia.org/wiki/Media_aritm%C3%A9tica

https://definicion.de/promedio/

https://www.google.com.mx/search?q=promedio+ejemplos&tbm=isch&ved=2ahUKEwiw6d_9_tLeAhWO2p8KHZuOCjoQ2-cCegQIABAC&oq=promedio+ej&gs_l=mobile-gws-wiz-img.1.0.0l4j0i5i30.49383.52508..55628...0.0..0.193.489.0j3......0....1.........0i67.7bfY5DAZtpo&ei=OJ3rW7BtjrX_BJudqtAD&client=ms-android-americamovil-mx&prmd=ivn&biw=320&bih=452