MEDIDAS DE DISPERSIÓN PARA DATOS SIMPLES Y AGRUPADOS
Las medidas de dispersión nos permiten conocer si los valores en general están cerca o alejados de los valores centrales, muestran la variabilidad de una distribución de datos, indicando por medio de un número si las diferentes puntuaciones de una variable están muy alejadas de la medida de tendencia central.
RANGO
Es la diferencia entre el valor máximo y el mínimo en nuestros datos, esta medida de dispersión aunque es la más fácil de obtener, en lo general es muy poco usada.
Datos agrupados Hay dos formas para determinar el rango para datos agrupados:
1) Rango = punto medio de la clase más alta – punto medio de la más baja
2) Rango = límite superior de la clase más alta – límite inferior de la más baja.
EJEMPLO:
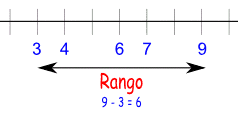
En {4, 6, 9, 3, 7} el menor valor es 3, y el mayor es 9, entonces el rango es 9-3 igual a 6.
Rango puede significar también todos los valores de resultado de una función.
Rango puede significar también todos los valores de resultado de una función.
DESVIACIÓN MEDIA
La desviación media o desviación promedio es abreviada por MD. Mide la desviación promedio de valores con respecto a la media del grupo, sin tomar en cuenta el signo de la desviación.
EJEMPLO:

Vamos a utilizar tablas, ya que así el procedimiento para calcular la desviación media te sirve para cuando tengas muchos datos y para cuando tengas pocos.
En primer lugar, ordenamos los datos en una tabla con la frecuencia absoluta de cada uno de ellos, dejando la última fila para la suma total de elementos de datos:
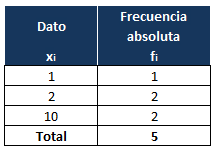
Vamos a empezar calculando la media, ya que la necesitamos para obtener las desviaciones. Añadimos una tercera columna para escribir el resultado de multiplicar cada dato por su frecuencia absoluta. En la última fila sumamos los resultados:

Ya tenemos los datos que necesitamos para calcular la media, según la fórmula, que son la suma de las multiplicaciones de cada dato por su frecuencia absoluta y el número total de datos:

La suma de las multiplicaciones de los datos por la frecuencia absoluta es 25 y lo tenemos en la última fila de la tercera columna. El número total de datos es 5 y lo tenemos al final de la segunda columna:

La media es 5.
Una vez tenemos la media, ya podemos calcular la distancia o la desviación de cada dato, como el valor absoluta de la diferencia entre cada dato con la media:
Para ello, añadimos una cuarta columna donde iremos escribiendo la distancia de cada dato:
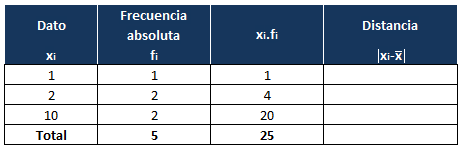
Por ejemplo, para el dato 1, la distancia sería:
Lo hacemos igual para el resto de datos y los vamos escribiendo en la columna. En la última fila, realizamos la suma de todas las distancias:
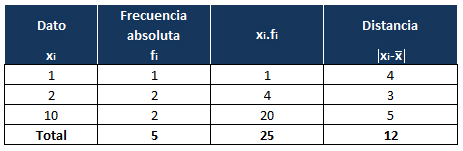
Ya tenemos los datos que necesitamos para calcular la desviación media, según la fórmula, que son la suma de las distancias de cada dato y el número total de datos:
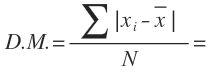
La suma de las distancias es 12 y lo tenemos en la última fila de la cuarta columna. El número total de datos es 5, que lo tenemos al final de la segunda columna:

DESVIACIÓN ESTÁNDAR
La desviación estándar o desviación típica (σ) es una medida de centralización o dispersión para variables de razón (ratio o cociente) y de intervalo, de gran utilidad en la estadística descriptiva.Se define como la raíz cuadrada de la varianza. Junto con este valor, la desviación típica es una medida (cuadrática) que informa de la media de distancias que tienen los datos respecto de su media aritmética, expresada en las mismas unidades que la variable.
EJEMPLO:
Tú y tus amigos habéis medido las alturas de vuestros perros (en milímetros):
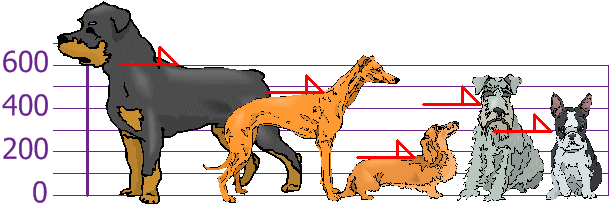

Las alturas (de los hombros) son: 600mm, 470mm, 170mm, 430mm y 300mm.
Calcula la media, la varianza y la desviación estándar.
Respuesta:
| Media = |
600 + 470 + 170 + 430 + 300
| = |
1970
| = 394 |
5
|
5
|
así que la altura media es 394 mm. Vamos a dibujar esto en el gráfico:
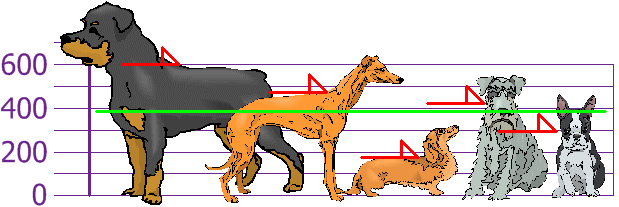

Ahora calculamos la diferencia de cada altura con la media:
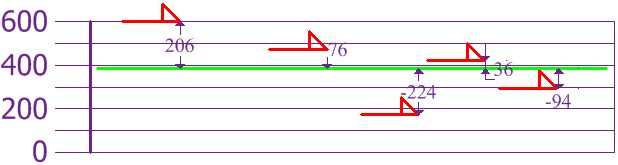

Para calcular la varianza, toma cada diferencia, elévala al cuadrado, y haz la media:
| Varianza: σ2 = |
2062 + 762 + (-224)2 + 362 + (-94)2
| = |
108,520
| = 21,704 |
5
|
5
|
Así que la varianza es 21,704.
Y la desviación estándar es la raíz de la varianza, así que:
Desviación estándar: σ = √21,704 = 147
y lo bueno de la desviación estándar es que es útil: ahora veremos qué alturas están a distancia menos de la desviación estándar (147mm) de la media:
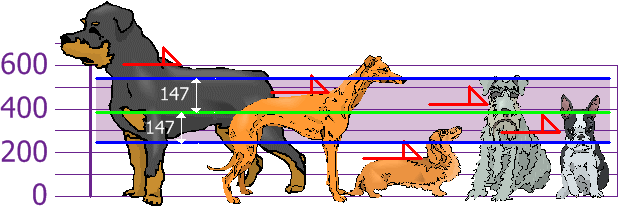

Así que usando la desviación estándar tenemos una manera "estándar" de saber qué es normal, o extra grande o extra pequeño.
VARIANZA
Es una medida estadística que mide la dispersión de los valores respecto a un valor central (media), es decir, es el cuadrado de las desviaciones.
Es una medida estadística que mide la dispersión de los valores respecto a un valor central (media), es decir, es el cuadrado de las desviaciones.
BIBLIOGRAFIA:
http://www.disfrutalasmatematicas.com/datos/desviacion-estandar.html
https://ekuatio.com/medidas-de-dispersion-recorrido-desviacion-media-varianza-y-desviacion-tipica/
http://www.disfrutalasmatematicas.com/definiciones/rango-estadistica-.html
https://prezi.com/obxa6mstewuk/medidas-de-dispersion-para-datos-agrupados/

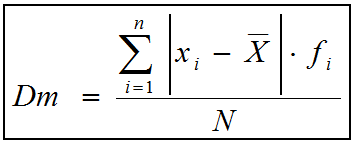



Muy buena Explicación, Gracias!!!
ResponderBorrarMessirve
ResponderBorrarGracias :D con esto hice mi actividad para estadistica
ResponderBorrarehhh podria enseñar cual es la respuesta a la tabla de ese que dice amigo A
ResponderBorrar