ELEMENTOS ESTADÍSTICOS:

ESTADÍSTICA

Es la rama de las matemáticas que estudia la variabilidad, así como el proceso aleatorio que la genera siguiendo leyes de probabilidad.Se ocupa de recoger y obtener datos para posteriormente analizar y obtener alguna conclusión válida de ellos y tomar decisiones respecto a esas conclusiones.

Se divide en dos grupos:

• Estadística descriptiva: se dedica a los métodos de recolección, descripción, visualización y resumen de datos originados a partir de los fenómenos de estudio. Los datos pueden ser resumidos numérica o gráficamente. Ejemplos básicos de parámetros estadísticos son: la media y la desviación estándar. Algunos ejemplos gráficos son: histograma, pirámide población, clústers, entre otros.
  

 INVESTIGACIÓN ESTADÍSTICA:

• Estadística inferencial: se dedica a la generación de los modelos, inferencias y predicciones asociadas a los fenómenos en cuestión teniendo en cuenta la aleatoriedad de las observaciones. Se usa para modelar patrones en los datos y extraer inferencias acerca de la población bajo estudio. Estas inferencias pueden tomar la forma de respuestas a preguntas si/no (prueba de hipótesis), estimaciones de características numéricas (estimación), pronósticos de futuras observaciones, descripciones de asociación (correlación) o modelamiento de relaciones entre variables (análisis de regresión). Otras técnicas de modelamiento incluyen anova, series de tiempo y minería de datos.

POBLACIÓN

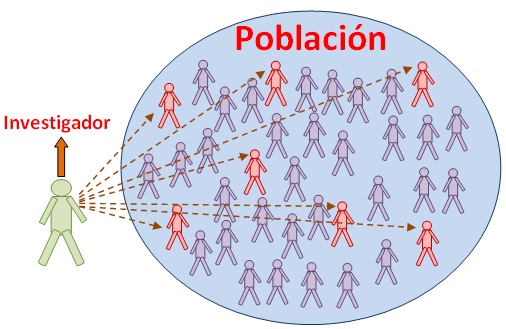
Término utilizado en estadística para denominar al conjunto de elementos de referencia sobre el que se realizan las observaciones. A este conjunto también se le denomina universo o colectivo.

La población en sentido demográfico es un conjunto de individuos (todos los habitantes de un país, todas las ratas de una ciudad, entre otros), mientras que una población en sentido estadístico es un conjunto de datos referidos a determinada característica o atributo de los individuos (las edades de todos los individuos de un país, el color de todas las ratas de una ciudad, entre otros).

La población estadística es una variable aleatoria relacionada con los objetos o individuos que se pretende estudiar en una investigación. Cada uno de los elementos de la población se denomina individuo y estos comparten algunas características.

Puede ser un grupo de objetos/personas realmente existentes (por ejemplo, el conjunto de todas las personas de un pueblo) o un grupo hipotético y potencialmente infinito de objetos concebidos como una generalización (por ejemplo, el conjunto de todas las jugadas posibles en ajedrez).

EJEMPLO: Lugar que ocupa en un viñedo cada planta, la altura de cada árbol, numero de racimos por planta, edad de cada una de las plantas, producción de uva por árbol.

Población física: está compuesta por todos los individuos o elementos que proporcionarán la información a través de la cual se realizará el estudio y el análisis. Los integrantes de una población física pueden ser personas, seres vivos de cualquier especie, objetos, entidades, instituciones; en fin, todo conjunto de elementos que sean posibles de ser medidos.

EJEMPLO:

Todos los alumnos del Colegio de Bachilleres del Estado de PUEBLA.

 • Algunas poblaciones estadísticas asociadas: Las estaturas de todos los alumnos, los pesos de todos los estudiantes, las edades de todos los jóvenes del Colegio, el tipo de sangre de cada uno de los alumnos del Colegio, el número de hermanos de todos los alumnos inscritos en el Colegio, ETC.

Muestra

Subcolección de elementos de una población. Se le conoce como tamaño de muestra al número de datos que la conforman y se representa con la letra “n”.

 • En todo estudio estadístico es muy importante especificar la población de la cual fue extraída la muestra.

 EJEMPLO: Si el objetivo es conocer las carreras universitarias preferidas por los futuros egresados del Colegio de Bachilleres del Estado de PUEBLA; debido a lo complicado de realizar un censo, se elige al azar una muestra de 50 alumnos de cada uno de los 23 planteles existentes

• Variable: Es toda aquella característica que poseen todos los elementos de una población física y que pueden diferir del valor que pueda tomar. Las variables permiten clasificar a los individuos, objetos, entidades, en los que se mide la característica. Las variables son la herramienta fundamental de la estadística, debido a que el análisis estadístico de la información se realiza principalmente sobre los valores de las variables. 

• TIPOS DE VARIABLES:

• Cualitativa (o categórica): son las variables que pueden tomar como valores cualidades o categorías.
  Ejemplos:
  • Sexo (hombre, mujer)
  • Salud (buena, regular, mala)
• Cuantitativas (o numérica): variables que toman valores numéricos.
  Ejemplos:
  • Número de casas (1, 2,…). Discreta.
  • Edad (12,5; 24,3; 35;…). Continua.

Las variables cualitativas (o variables categóricas) se pueden clasificar según sigan una jerarquía o un orden determinado.

VARIABLES CUALITATIVAS

Tipos	Definición	Ejemplos
Nominal	Variables cualitativa cuyas categorías no siguen ningún orden.	– Color (blanco, rojo, azul,…) – Lateralidad (zurdo, diestro)
Ordinal	Son las variables categóricas con orden o jerarquía	– Nota examen (suspenso, aprobado, notable, sobresaliente) – Nivel económico (pobre, clase media, rico) – Medalla deportiva (Oro, plata, bronce)

Las variables cuantitativas se clasifican según el número de valores que puede tomar la variable.

VARIABLES CUANTITATIVAS

Tipos	Definición	Ejemplos
Discreta	La variable solo puede tomar valores en número determinado de valores. En cada intervalo de valores la variable solo puede tomar un valor.	– Canastas en un partido (20; 21; 22; pero no 21,5) – Hijos por familia (0, 1, 2, 3,…)
Continua	La variable puede adquirir cualquier valor dentro de un intervalo de valores determinado.	– Peso (53,53 kg; 89,4 kg,…)

BIBLIOGRAFIA:

https://prezi.com/zorz53lcley6/principales-elementos-de-la-estadistica/

https://es.slideshare.net/florisabels/cuales-son-los-elementos-fundamentales-de-la-estadstica

https://carmesimatematic.webcindario.com/estadisticamat.htm

https://ekuatio.com/apuntes-de-matematicas/estadistica-probabilidad/conceptos-basicos-de-estadistica-ejemplos/