LIMITES ESTADÍSTICOS
Son aquellas entidades numéricas utilizadas para señalar la posición que ocupa un dato determinado, en relación con el resto de datos numéricos, permitiendo así conocer otros puntos propios de la distribución de datos, que no son inherentes a los valores centrales.
Ente los que se encuentran:











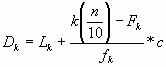






 Cuando n es par:
Cuando n es par:
 Cuando n es impar:
Cuando n es impar:








 Cuando n es impar:
Cuando n es impar:

 La posición del primer cuartil.
La posición del primer cuartil.


 El primer cuartil:
El primer cuartil:





CUARTILES
Los cuartiles son los tres valores que dividen al conjunto de datos ordenados en cuatro partes porcentualmente iguales.
Hay tres cuartiles denotados usualmente Q1, Q2, Q3. El segundo cuartil es precisamente la mediana. El primer cuartil, es el valor en el cual o por debajo del cual queda un cuarto (25%) de todos los valores de la sucesión (ordenada); el tercer cuartil, es el valor en el cual o por debajo del cual quedan las tres cuartas partes (75%) de los datos.
Datos Agrupados

Como los cuartiles adquieren su mayor importancia cuando contamos un número grande de datos y tenemos en cuenta que en estos casos generalmente los datos son resumidos en una tabla de frecuencia. La fórmula para el cálculo de los cuartiles cuando se trata de datos agrupados es la siguiente:
k= 1,2,3
Donde:
Lk = Límite real inferior de la clase del cuartil k
n = Número de datos
Fk = Frecuencia acumulada de la clase que antecede a la clase del cuartil k.
fk = Frecuencia de la clase del cuartil k
c = Longitud del intervalo de la clase del cuartil k
Si se desea calcular cada cuartil individualmente, mediante otra fórmula se tiene lo siguiente:
- El primer cuartil Q1, es el menor valor que es mayor que una cuarta parte de los datos; es decir, aquel valor de la variable que supera 25% de las observaciones y es superado por el 75% de las observaciones.
Fórmula de Q1, para series de Datos agrupados:
Donde:
L1 = limite inferior de la clase que lo contiene
P = valor que representa la posición de la medida
f1 = la frecuencia de la clase que contiene la medida solicitada.
Fa-1 = frecuencia acumulada anterior a la que contiene la medida solicitada.
Ic = intervalo de clase
- El segundo cuartil Q2, (coincide, es idéntico o similar a la mediana, Q2 = Md), es el menor valor que es mayor que la mitad de los datos, es decir el 50% de las observaciones son mayores que la mediana y el 50% son menores.
Fórmula de Q2, para series de Datos agrupados:
Donde:
L1 = limite inferior de la clase que lo contiene
P = valor que representa la posición de la medida
f1 = la frecuencia de la clase que contiene la medida solicitada.
Fa-1 = frecuencia acumulada anterior a la que contiene la medida solicitada.
Ic = intervalo de clase
- El tercer cuartil Q3, es el menor valor que es mayor que tres cuartas partes de los datos, es decir aquel valor de la variable que supera al 75% y es superado por el 25% de las observaciones.
Fórmula de Q3, para series de Datos agrupados:
Donde:
L1 = limite inferior de la clase que lo contiene
P = valor que representa la posición de la medida
f1 = la frecuencia de la clase que contiene la medida solicitada.
Fa-1 = frecuencia acumulada anterior a la que contiene la medida solicitada.
Ic = intervalo de clase.
Otra manera de verlo es partir de que todas las medidas no son sino casos particulares del percentil, ya que el primer cuartil es el 25% percentil y el tercer cuartil 75% percentil.
Para Datos No Agrupados
Si se tienen una serie de valores X1, X2, X3 ... Xn, se localiza mediante las siguientes fórmulas:
- El primer cuartil:
Cuando n es par:
Cuando n es impar:
- Para el tercer cuartil
Cuando n es par:
Cuando n es impar:
Los deciles son ciertos números que dividen la sucesión de datos ordenados en diez partes porcentualmente iguales. Son los nueve valores que dividen al conjunto de datos ordenados en diez partes iguales, son también un caso particular de los percentiles. Los deciles se denotan D1, D2,..., D9, que se leen primer decil, segundo decil, etc.
Los deciles, al igual que los cuartiles, son ampliamente utilizados para fijar el aprovechamiento académico.
Datos Agrupados
Para datos agrupados los deciles se calculan mediante la fórmula.
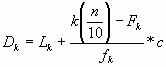
k= 1,2,3,... 9
Donde:
Lk = Límite real inferior de la clase del decil k
n = Número de datos
Fk = Frecuencia acumulada de la clase que antecede a la clase del decil k.
fk = Frecuencia de la clase del decil k
c = Longitud del intervalo de la clase del decil k
Otra fórmula para calcular los deciles:
- El cuarto decil, es aquel valor de la variable que supera al 40%, de las observaciones y es superado por el 60% de las observaciones.
- El quinto decil corresponde a la mediana.
- El noveno decil supera al 90% y es superado por el 10% restante.
Donde (para todos):
L1 = limite inferior de la clase que lo contiene
P = valor que representa la posición de la medida
f1 = la frecuencia de la clase que contiene la medida solicitada.
Fa-1 = frecuencia acumulada anterior a la que contiene la medida solicitada.
Ic = intervalo de clase.
Fórmulas Datos No Agrupados
Si se tienen una serie de valores X1, X2, X3 ... Xn, se localiza mediante las siguientes fórmulas:
Siendo A el número del decil.
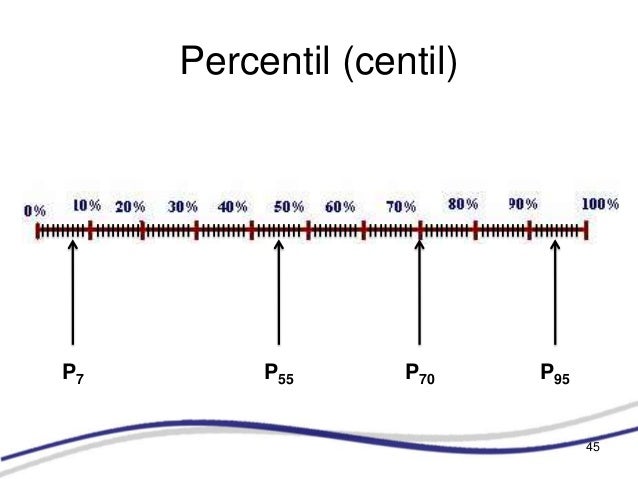
Los percentiles son, tal vez, las medidas más utilizadas para propósitos de ubicación o clasificación de las personas cuando atienden características tales como peso, estatura, etc.
Los percentiles son ciertos números que dividen la sucesión de datos ordenados en cien partes porcentualmente iguales. Estos son los 99 valores que dividen en cien partes iguales el conjunto de datos ordenados. Los percentiles (P1, P2,... P99), leídos primer percentil,..., percentil 99.
Datos Agrupados
Cuando los datos están agrupados en una tabla de frecuencias, se calculan mediante la fórmula:

k= 1,2,3,... 99
Donde:
Lk = Límite real inferior de la clase del decil k
n = Número de datos
Fk = Frecuencia acumulada de la clase que antecede a la clase del decil k.
fk = Frecuencia de la clase del decil k
c = Longitud del intervalo de la clase del decil k
Otra forma para calcular los percentiles es:
- Primer percentil, que supera al uno por ciento de los valores y es superado por el noventa y nueve por ciento restante.
- El 60 percentil, es aquel valor de la variable que supera al 60% de las observaciones y es superado por el 40% de las observaciones.
- El percentil 99 supera 99% de los datos y es superado a su vez por el 1% restante.
Fórmulas Datos No Agrupados
Si se tienen una serie de valores X1, X2, X3 ... Xn, se localiza mediante las siguientes fórmulas:
Para los percentiles, cuando n es par:
Siendo A, el número del percentil.
Es fácil ver que el primer cuartil coincide con el percentil 25; el segundo cuartil con el percentil 50 y el tercer cuartil con el percentil 75.
Determinación del primer cuartil, el séptimo decil y el 30 percentil, de la siguiente tabla:
Salarios
|
No. De
|
fa
|
(I. De Clases)
|
Empleados (f1)
| |
200-299
|
85
|
85
|
300-299
|
90
|
175
|
400-499
|
120
|
295
|
500-599
|
70
|
365
|
600-699
|
62
|
427
|
700-800
|
36
|
463
|
Como son datos agrupados, se utiliza la fórmula
Siendo,
La posición del 7 decil.
La posición del percentil 30.
Entonces,
115.5 – 85 = 30.75
Li = 300, Ic = 100 , fi = 90
El 7 decil:
Posición:
324.1 – 295 = 29.1
Li = 500, fi = 70
El percentil 30
Posición:
138.9 – 85 = 53.9
fi = 90
Estos resultados nos indican que el 25% de los empleados ganan salarios por debajo de $ 334; que bajo 541.57 gana el 57%de los empleados y sobre $359.88, gana el 70% de los empleados.
BIBLIOGRAFIA:
https://www.monografias.com/trabajos27/datos-agrupados/datos-agrupados.shtml
https://ekuatio.com/apuntes-de-matematicas/estadistica-probabilidad/conceptos-basicos-de-estadistica-ejemplos/
https://es.slideshare.net/AXELALEXIZ/estadistica-sumatoriamtcymd